Particle Shape Analysis of Polystyrene Spheres
Polystyrene spheres are widely utilized as calibration standards in particle size and shape analysis due to their uniformity and well-defined dimensions. Accurate characterization of these spheres is essential for ensuring the precision of analytical instruments and methodologies.
Objective – Accurate measurement of spheres
This application note aims to generate precise size distributions for polystyrene spheres, with diameters ranging from 3 to 125 microns. Utilizing the Pi Sentinel PRO, we measure number, surface area, and volume weighting to achieve this goal.
Methodology – Size and Shape measurement of spheres
The Pi Sentinel PRO employs dynamic image analysis to capture high-resolution images of dispersed polystyrene spheres. Advanced algorithms process these images to determine particle size and shape parameters accurately.

Typical Images from the Pi Sentinel PRO Particle Shape Analyzer.

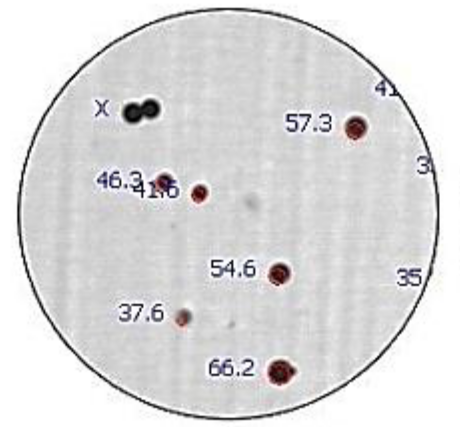
ECA Diameter

Circularity
Notes
Results
The analysis provides detailed size distributions, including number-based, surface area-based, and volume-based metrics. This comprehensive data ensures a thorough understanding of the particle characteristics.
Equivalent Circular Area Diameter, which is the logical measure to use with spheres, is the diameter of a circle which shares an equivalent projected area with the actual particle. Beads habitually bunch together, and the real challenge is eliminating these clusters from the analysis. However, by implementing shape rejection, any entity possessing a circularity value under 0.80 is disregarded.
In the sample diagram, there is a double displaying a circularity of 0.626 (shape rejection was momentarily suspended to reveal the value). Fortunately, this cluster is avoided in the actual data acquisition stage.
Results
The Equivalent Circular Area Diameter histogram graph demonstrates that the particles do not form a straightforward, conventional distribution; on the left side, there is a tail of smaller particles, and a secondary peak at about 60 microns. The desirable (in-focus) particles varied in size from 3.9 to 124.4 microns. The average, in this instance 38.1, is typically implemented as a “single number” sample representation.
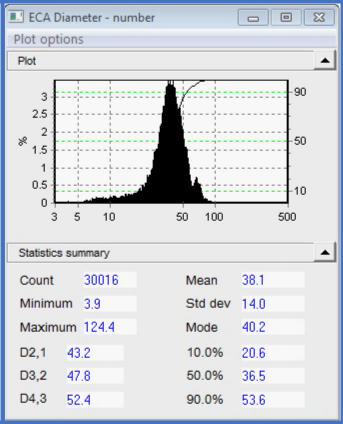
The percentiles (10%, 50%, 90%) offer further information regarding how the data is scattered around the average. Compared to a linear axis, the logarithmic size axis provides a superior visual characterization of the distribution nearer the low end. It can do this by “stretching out” the lower end.
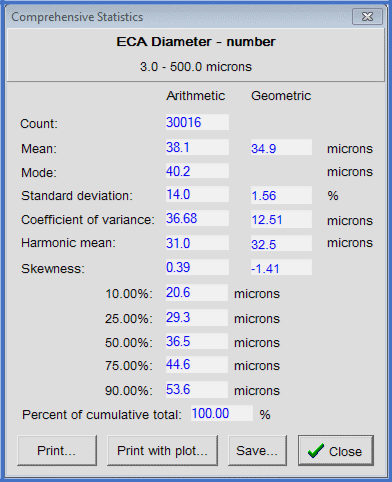
The Comprehensive Statistics designate the sample with even more precision, with the use of established statistics for histogram data. The Arithmetic values derive from the initial data, corresponding visually with how the histogram would be represented on a linear size axis. The geometric statistics provide a visual representation of the log axis distribution; the graph is slanted right in one instance, and left in the other, for example.
This Circularity plot displays the circularity histogram. An inspection of particle thumbnail images demonstrates that the counts of less than 0.8 constitute clusters of spheres. However, after shape rejection is established to disregard objects embodying a circularity below 0.8, this section of the circularity histogram ceases to exist. In the size graph, if the small peak of 60 microns disappears following shape rejection, it can be concluded that it constitutes those particle clusters.
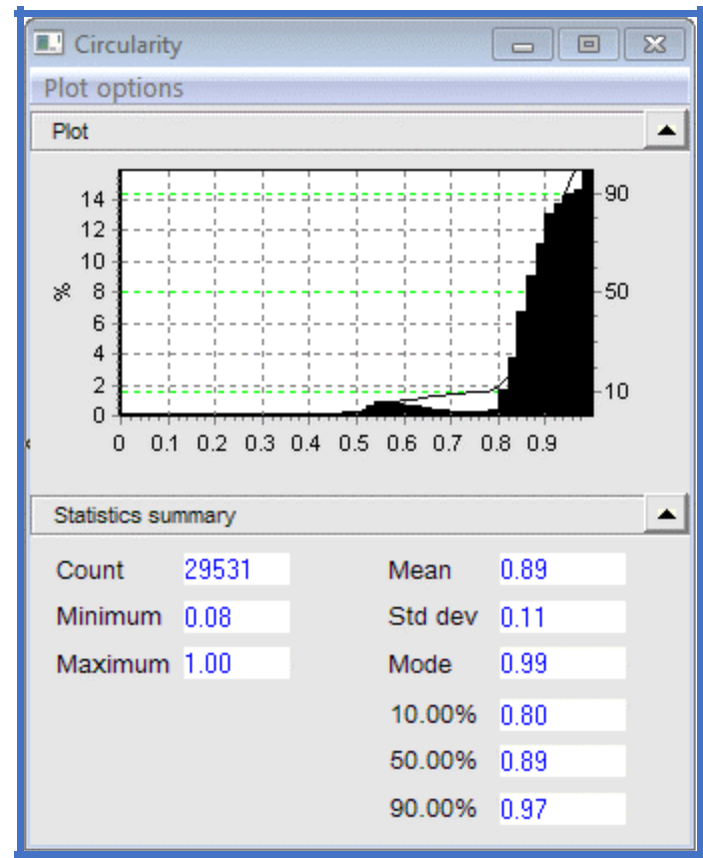
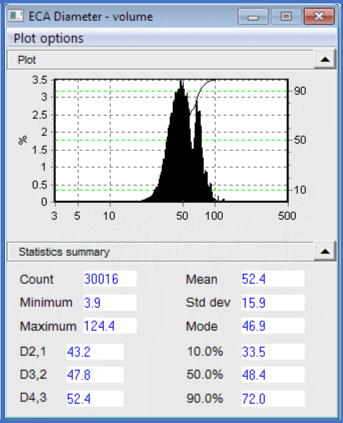
The volume graph exhibits equivalent results, albeit to a much greater magnitude. Volume weighting is utilized when the volume of individual particles significantly impacts upon outcomes, such as in certain chemical reactions. If the distribution is plotted according to surface area, the low-end tail ceases to exist, because those particles yield a minimal contribution to the aggregate surface area. The small peak at 60 is more prominent, because it now embodies a larger proportion of the sample surface area. The entire distribution transfers moderately to the right. A more practical example for the user of Volume weighted histograms is to point out any agglomerates in a sample. If agglomerates are rarely detected, then Number Weighted histograms will likely not point them out, but Volume histograms will.
Conclusion
Dynamic image analysis, as implemented in the Pi Sentinel PRO, offers a robust and precise method for characterizing polystyrene spheres. This technique ensures accurate particle size and shape analysis, which is crucial for applications requiring high precision.

